This math topic focuses on comparing fractions without changing their denominators. It includes exercises where students choose the appropriate relation (less than, greater than, or equal to) between pairs of fractions that share the same denominator. This skill is essential for understanding how fractions represent numbers and their relative sizes. Each question presents two fractions, and students must select the correct inequality symbol to describe their relationship. This is a part of a broader introductory unit on comparing fractions.
Work on practice problems directly here, or download the printable pdf worksheet to practice offline.
moreFraction Comparison - Mixed - No Changed Denominator Worksheet

| Math worksheet on 'Fraction Comparison - Mixed - No Changed Denominator (Level 3)'. Part of a broader unit on 'Fraction Comparing - Intro' Learn online: app.mobius.academy/math/units/fractions_comparing_intro/ |
1

| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
2
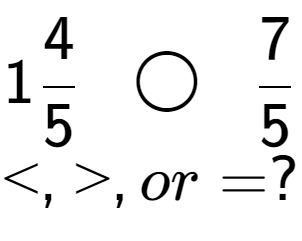
| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
3

| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
4
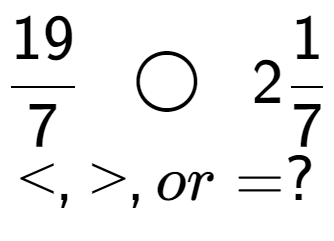
| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
5
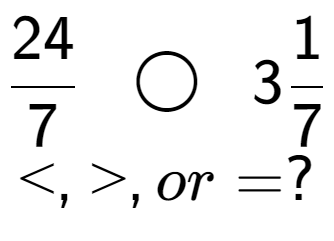
| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
6

| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |
7

| Compare these fractions and choose the right equality operator |
a
| < |
b
| > |
c
| = |