Home
Grade 1Grade 2Grade 3Grade 4Grade 5Grade 6Grade 7Grade 8Grade 9Grade 10Grade 11Math Themes
Explorers (Grades 1-3)Explorers Elite (1-3)Navigators (Grades 4-6)Navigators Elite (4-6)Challengers (Grades 7-9)Challengers Elite (7-9)Schedule an Evaluation
Mobius MethodFlexible ClassesCompanySupport
Pricing
Ctrl+k
Sign InJoin
Function Domain - Fraction Integer over Linear to Domain Definition

Level 1

This math topic focuses on determining the domain of rational functions, where the denominator includes a linear expression. The students are provided with functions of the form \( f(x) = \frac{a}{bx+c} \), and they must identify the valid values of \( x \) that do not make the denominator zero, thereby avoiding undefined expressions. Each question presents a function with different coefficients in the linear denominator, and multiple-choice answers detail various potential domains using set notation and inequality symbols, testing the student's understanding of restrictions in rational functions.

Work on practice problems directly here, or download the printable pdf worksheet to practice offline.

more
View

Function Domain - Fraction Integer over Linear to Domain Definition Worksheet

Mobius Math Academy logo
Math worksheet on 'Function Domain - Fraction Integer over Linear to Domain Definition (Level 1)'. Part of a broader unit on 'Functions - Domain and Range Solving - Practice' Learn online: app.mobius.academy/math/units/functions_domain_range_solving_practice/
1
What set describes the domain of this function?
A LaTex expression showing f(x) = -3 over -1x-5
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -5\text{{ or }}-5 < X\}
b A LaTex expression showing \{X \in \mathbb{{R}} \vert X \le -5\text{{ or }}-5 \le X\}
2
What set describes the domain of this function?
A LaTex expression showing f(x) = -2 over -1x+4
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X < 4\text{{ or }}4 < X\}
b A LaTex expression showing \{X \in \mathbb{{R}} \vert -4 < X < 4\text{{ or }}-4 < X < 4\}
3
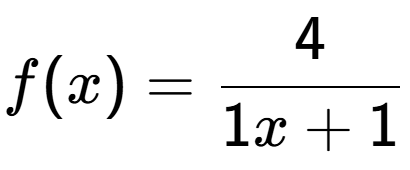
What set describes the domain of this function?
A LaTex expression showing f(x) = 4 over 1x+1
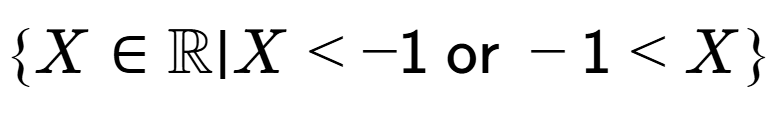
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -1\text{{ or }}-1 < X\}
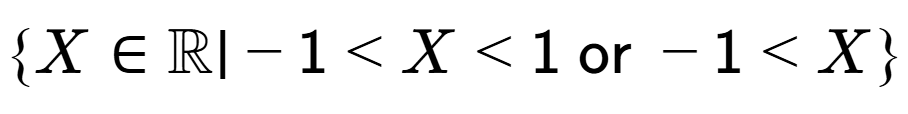
b A LaTex expression showing \{X \in \mathbb{{R}} \vert -1 < X < 1\text{{ or }}-1 < X\}
4
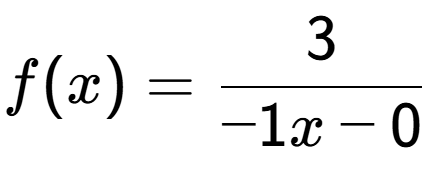
What set describes the domain of this function?
A LaTex expression showing f(x) = 3 over -1x-0
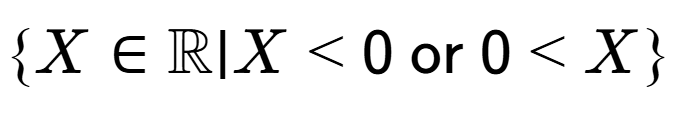
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X < 0\text{{ or }}0 < X\}
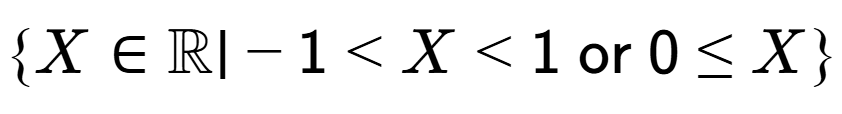
b A LaTex expression showing \{X \in \mathbb{{R}} \vert -1 < X < 1\text{{ or }}0 \le X\}
5
What set describes the domain of this function?
A LaTex expression showing f(x) = 4 over 1x+3
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -3\text{{ or }}-3 < X < 3\}
b A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -3\text{{ or }}-3 < X\}
6
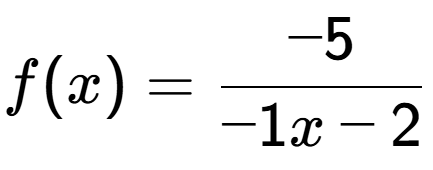
What set describes the domain of this function?
A LaTex expression showing f(x) = -5 over -1x-2
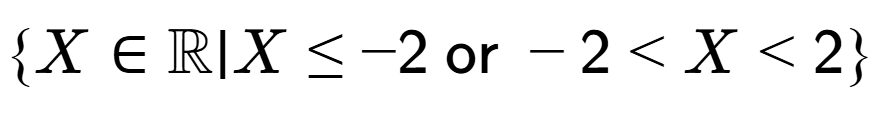
a A LaTex expression showing \{X \in \mathbb{{R}} \vert X \le -2\text{{ or }}-2 < X < 2\}
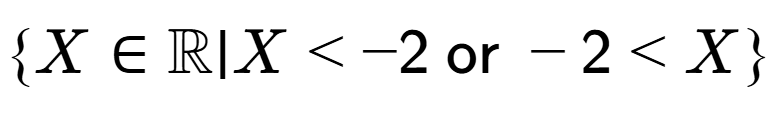
b A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -2\text{{ or }}-2 < X\}
7
What set describes the domain of this function?
A LaTex expression showing f(x) = 5 over 1x+3
a A LaTex expression showing \{X \in \mathbb{{R}} \vert -3 < X < 3\text{{ or }}-3 < X < 3\}
b A LaTex expression showing \{X \in \mathbb{{R}} \vert X < -3\text{{ or }}-3 < X\}