This math topic focuses on calculating the perimeter of various geometric shapes, primarily rectangles, by determining how many smaller segments are required to wrap around a larger shape. The skill practiced involves division and multiplication, applying the concept of perimeter in a practical context. Each problem presents a different shape and set of possible answers, where students must analyze the illustration and calculate how many units of a given smaller segment fit into the total perimeter of the larger shape. This area of study is part of a broader introduction to area and perimeter logic.
Work on practice problems directly here, or download the printable pdf worksheet to practice offline.
morePerimeter of a Rectangle - Segment Coverage from Perimeter Worksheet

| Math worksheet on 'Perimeter of a Rectangle - Segment Coverage from Perimeter (Level 2)'. Part of a broader unit on 'Area and Perimeter Logic - Intro' Learn online: app.mobius.academy/math/units/area_and_perimeter_geometry_logic_intro/ |
1
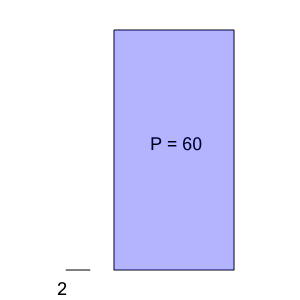
| How many of the small line segment will it take to wrap around the larger shape? |
a
| 30 |
b
| 18 |
c
| 54 |
d
| 15 |
e
| 57 |
f
| 12 |
2

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 29 |
b
| 50 |
c
| 32 |
d
| 44 |
e
| 41 |
f
| 26 |
3

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 46 |
b
| 36 |
c
| 12 |
d
| 20 |
e
| 18 |
f
| 28 |
4

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 16 |
b
| 22 |
c
| 6 |
d
| 2 |
e
| 20 |
f
| 24 |
5

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 14 |
b
| 24 |
c
| 26 |
d
| 28 |
e
| 16 |
f
| 38 |
6

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 38 |
b
| 36 |
c
| 6 |
d
| 20 |
e
| 10 |
f
| 22 |
7

| How many of the small line segment will it take to wrap around the larger shape? |
a
| 14 |
b
| 22 |
c
| 20 |
d
| 26 |
e
| 32 |
f
| 4 |