Home
Grade 1Grade 2Grade 3Grade 4Grade 5Grade 6Grade 7Grade 8Grade 9Grade 10Grade 11Math Themes
Explorers (Grades 1-3)Explorers Elite (1-3)Navigators (Grades 4-6)Navigators Elite (4-6)Challengers (Grades 7-9)Challengers Elite (7-9)Schedule an Evaluation
Mobius MethodFlexible ClassesCompanySupport
Pricing
Ctrl+k
Sign InJoin
Radicals

Divide Binomials by Monomials (Values and Variables) (Level 1)

This math topic focuses on dividing radical expressions where binomials are divided by monomials, involving both numerical and algebraic expressions. The problems require simplification of the resulting expressions following the division. Each question presents a radical binomial expression in the numerator and a monomial in the denominator. Multiple-choice answers suggest the students need to select the correct simplified form, highlighting skills in manipulating square roots, variables, and rationalizing the denominator where applicable.

Work on practice problems directly here, or download the printable pdf worksheet to practice offline.

more
View

Radicals - Divide Binomials by Monomials (Values and Variables) Worksheet

Mobius Math Academy logo
Math worksheet on 'Radicals - Divide Binomials by Monomials (Values and Variables) (Level 1)'. Part of a broader unit on 'Radicals - Division Intro' Learn online: app.mobius.academy/math/units/radicals_division_intro/
1
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{{p} to the power of 2 square root of 11 - 2}{square root of 7p}
a A LaTex expression showing \frac{psquare root of 77p - 2square root of 7p}{7{p} to the power of -1 }
b A LaTex expression showing \frac{{p} to the power of 2 square root of 77p - 2square root of 7p}{7p}
c A LaTex expression showing \frac{{p} to the power of 2 square root of 77p + square root of 7p}{7{p} to the power of 3 }
d A LaTex expression showing \frac{{p} to the power of 2 square root of 77p + 4square root of 7p}{7{p} to the power of 3 }
e A LaTex expression showing \frac{psquare root of 77p + 2square root of 7}{3}
2
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{csquare root of 11 + 2{c} to the power of 2 }{csquare root of 11}
a A LaTex expression showing \frac{11 + 2{c} to the power of 3 square root of 11}{5}
b A LaTex expression showing 3 - 2csquare root of 11
c A LaTex expression showing \frac{11 - 3csquare root of 11}{22}
d A LaTex expression showing \frac{11 + 2square root of 11}{5}
e A LaTex expression showing \frac{11 + 2csquare root of 11}{11}
3
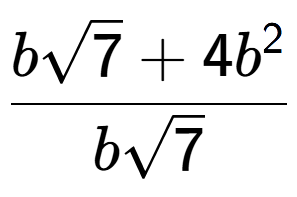
Divide the radical expressions and simplify the answer
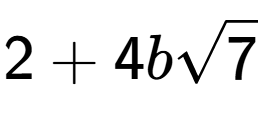
A LaTex expression showing \frac{bsquare root of 7 + 4{b} to the power of 2 }{bsquare root of 7}
a A LaTex expression showing 2 + 4bsquare root of 7
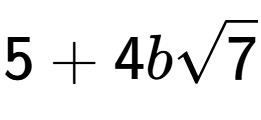
b A LaTex expression showing 5 + 4bsquare root of 7
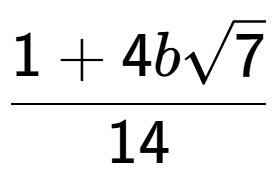
c A LaTex expression showing \frac{1 + 4bsquare root of 7}{14}
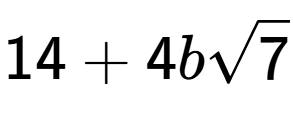
d A LaTex expression showing 14 + 4bsquare root of 7
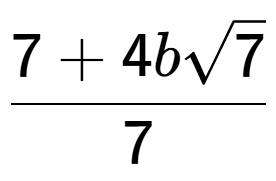
e A LaTex expression showing \frac{7 + 4bsquare root of 7}{7}
4
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{bsquare root of 3b - 5}{{b} to the power of 2 square root of 3}
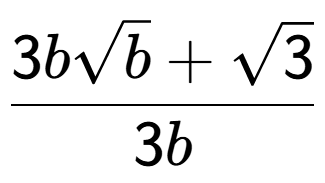
a A LaTex expression showing \frac{3bsquare root of b + square root of 3}{3b}
b A LaTex expression showing \frac{3bsquare root of b - square root of 3}{2{b} to the power of 2 }
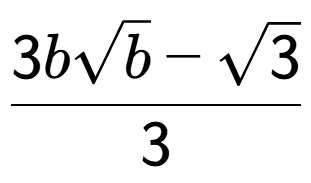
c A LaTex expression showing \frac{3bsquare root of b - square root of 3}{3}
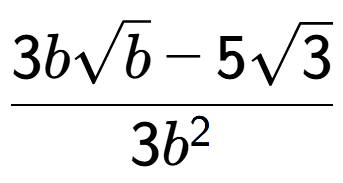
d A LaTex expression showing \frac{3bsquare root of b - 5square root of 3}{3{b} to the power of 2 }
e A LaTex expression showing \frac{2bsquare root of 3b - 15}{9{b} to the power of 2 }
5
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{2psquare root of p - psquare root of 13}{square root of 13p}
a A LaTex expression showing 2psquare root of 13 + 13square root of p
b A LaTex expression showing \frac{2{p} to the power of -1 square root of 13 + 13square root of p}{13}
c A LaTex expression showing 2psquare root of 13 - 13square root of 2p
d A LaTex expression showing \frac{2psquare root of 13 + 13p}{26}
e A LaTex expression showing \frac{2psquare root of 13 - 13square root of p}{13}
6
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{{y} to the power of 2 square root of 13 + 4ysquare root of y}{square root of 11y}
a A LaTex expression showing \frac{ysquare root of 143y + 4ysquare root of 11}{11}
b A LaTex expression showing ysquare root of 143y + 4y
c A LaTex expression showing \frac{{y} to the power of 2 square root of 143y + 4ysquare root of 11}{11}
d A LaTex expression showing ysquare root of 143y + 5ysquare root of 11
e A LaTex expression showing ysquare root of 143y + 4ysquare root of 11
7
Divide the radical expressions and simplify the answer
A LaTex expression showing \frac{5p - {p} to the power of 2 square root of 3}{square root of 7p}
a A LaTex expression showing 5square root of p + psquare root of 21p
b A LaTex expression showing \frac{5square root of 7p - psquare root of 21p}{7}
c A LaTex expression showing 5square root of 7p + {p} to the power of 2 square root of 21
d A LaTex expression showing \frac{5square root of 7p - {p} to the power of 3 square root of 21p}{5}
e A LaTex expression showing \frac{5square root of 14p - {p} to the power of 2 square root of 42p}{14}