Radicals - Divide Binomials by Monomials (Values and Variables) (Level 4)

Math worksheet on 'Radicals - Divide Binomials by Monomials (Values and Variables) (Level 4)'. Part of a broader unit on 'Radicals - Division Intro' Learn online: app.mobius.academy/math/units/radicals_division_intro/

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{4square root of 2 - {p} to the power of 2 {b} to the power of 2 square root of 11}{3{p} to the power of 2 square root of 13}$

a $A LaTex expression showing \frac{4square root of 26 - {p} to the power of 2 {b} to the power of 2 square root of 143}{39}$

b $A LaTex expression showing \frac{4square root of 26 - {p} to the power of 2 {b} to the power of 2 square root of 143}{39{p} to the power of 2 }$

c $A LaTex expression showing \frac{4 - {p} to the power of 2 {b} to the power of 2 square root of 143}{39p}$

d $A LaTex expression showing \frac{4square root of 78 + 2{p} to the power of 2 {b} to the power of 2 square root of 429}{117{p} to the power of 2 }$

e $A LaTex expression showing \frac{4square root of 26 + {p} to the power of 4 {b} to the power of 2 square root of 143}{{p} to the power of 2 }$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{3csquare root of 7cp - {c} to the power of 2 psquare root of 2}{4cpsquare root of 3cp}$

a $A LaTex expression showing \frac{3square root of 21 + csquare root of 6cp}{12{c} to the power of 2 p}$

b $A LaTex expression showing \frac{square root of 21 + square root of 6cp}{12p}$

c $A LaTex expression showing \frac{2square root of 21 - square root of 6cp}{12cp}$

d $A LaTex expression showing \frac{3square root of 21 - square root of 6cp}{12p}$

e $A LaTex expression showing \frac{square root of 21 + square root of 6cp}{2p}$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{bysquare root of 13 - 2ysquare root of 3b}{2{b} to the power of 2 ysquare root of 11}$

a $A LaTex expression showing \frac{bsquare root of 143 - 2square root of 33}{22{b} to the power of 2 }$

b $A LaTex expression showing \frac{bsquare root of 143 - 2square root of b}{{b} to the power of 2 }$

c $A LaTex expression showing \frac{bysquare root of 143 + 2square root of 33b}{5{b} to the power of 2 }$

d $A LaTex expression showing \frac{bsquare root of 143 - 2square root of 33b}{22{b} to the power of 2 }$

e $A LaTex expression showing \frac{bsquare root of 143 + square root of 33b}{22{b} to the power of 4 }$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{{y} to the power of 2 msquare root of 7 - 3msquare root of 13ym}{2{m} to the power of 2 square root of 5}$

a $A LaTex expression showing \frac{{y} to the power of 2 square root of 35 - 3ysquare root of 65ym}{10{m} to the power of 3 }$

b $A LaTex expression showing \frac{{m} to the power of -1 {y} to the power of 2 square root of 35 - 3square root of 65ym}{m}$

c $A LaTex expression showing \frac{{y} to the power of 2 square root of 35 - 3square root of 65ym}{10m}$

d $A LaTex expression showing \frac{{y} to the power of 2 square root of 35 + 3ysquare root of 65m}{10}$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{xpsquare root of 7x - 3xpsquare root of 13x}{2psquare root of 2xp}$

a $A LaTex expression showing \frac{xsquare root of 14p - 3xsquare root of 26p}{4p}$

b $A LaTex expression showing \frac{xsquare root of 14{p to the power of -1 } + 3xsquare root of 26p}{4{p} to the power of -1 }$

c $A LaTex expression showing \frac{{x} to the power of 2 square root of 14p - 3xsquare root of 26p}{4}$

d $A LaTex expression showing \frac{xsquare root of 14p + 3pxsquare root of 26p}{p}$

e $A LaTex expression showing \frac{xsquare root of 42 - 3xsquare root of 78p}{12p}$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{3ysquare root of 13y - {y} to the power of 2 square root of 13}{2ysquare root of 7m}$

a $A LaTex expression showing \frac{3square root of 91my + ysquare root of 91}{m}$

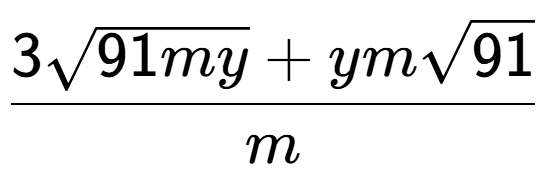
b $A LaTex expression showing \frac{3square root of 91my + ymsquare root of 91}{m}$

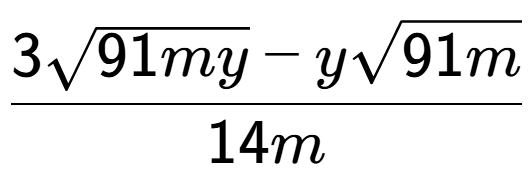
c $A LaTex expression showing \frac{3square root of 91my - ysquare root of 91m}{14m}$

d $A LaTex expression showing \frac{3square root of 91my - ysquare root of 91{m to the power of -1 }}{m}$

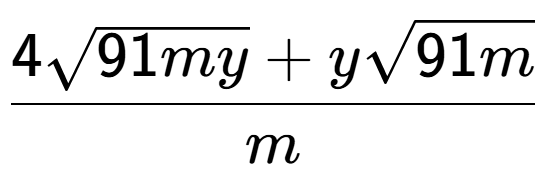
e $A LaTex expression showing \frac{4square root of 91my + ysquare root of 91m}{m}$

Divide the radical expressions and simplify the answer

$A LaTex expression showing \frac{pysquare root of 5y + 2pysquare root of 7}{2{p} to the power of 2 square root of 11y}$

a $A LaTex expression showing \frac{ysquare root of 55 + 2square root of 77y}{22p}$

b $A LaTex expression showing \frac{ysquare root of 55 - 2square root of 77{y to the power of -1 }}{22{p} to the power of 3 }$

c $A LaTex expression showing \frac{ysquare root of 55 + 2ysquare root of 77}{22{p} to the power of -1 }$

d $A LaTex expression showing \frac{ysquare root of 55 - 2square root of 77y}{22p}$

e $A LaTex expression showing \frac{{y} to the power of -1 square root of 55 - 2square root of 77y}{22py}$

Radicals - Divide Binomials by Monomials (Values and Variables) Worksheet