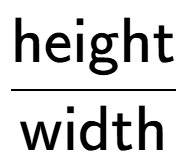This math topic focuses on introducing the concept of slope, interpreting slope as the ratio of rise to run (height to width). The problems provide real-world images, such as hills, slides, roofs, and ski jumps, asking how to calculate their slopes. Responses are given in the format of fraction equations, either as height over width or width over height, illustrating different perspectives on calculating slope. This basic introduction to slope helps learners understand and visualize the mathematical concept in daily contexts.
Work on practice problems directly here, or download the printable pdf worksheet to practice offline.
moreSlope Concept Intro Picture - Rise/Run Equation with Common Names Worksheet

| Math worksheet on 'Slope Concept Intro Picture - Rise/Run Equation with Common Names (Level 1)'. Part of a broader unit on 'Slope - Intro' Learn online: app.mobius.academy/math/units/slope_intro/ |
1

| How would you calculate the slope of this roof (slope is up/across)? |
a
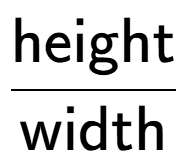
b
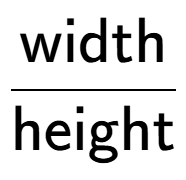
2

| How would you calculate the slope of this hill (slope is up/across)? |
a
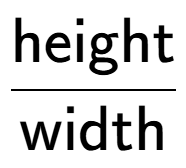
b
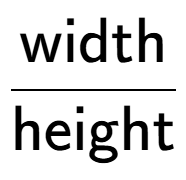
3

| How would you calculate the slope of this ski jump (slope is up/across)? |
a
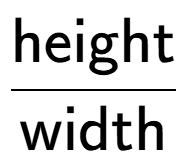
b
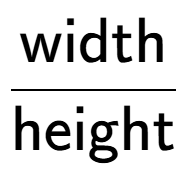
4

| How would you calculate the slope of this slide (slope is up/across)? |
a
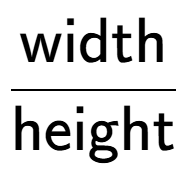
b