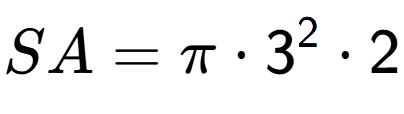This math topic focuses on calculating the surface area of cylinders. It involves applying formulas to determine the lateral and total surface areas using given dimensions (radius and height) for various cylinders. Each problem follows a consistent pattern, requiring students to use the formula \( SA = 2πrh + 2πr^2 \). This topic forms part of an advanced unit on the geometry of complex 3D shapes, enhancing students’ skills in handling π (Pi) in real-world geometrical applications.
Work on practice problems directly here, or download the printable pdf worksheet to practice offline.
moreSurface Area - Cylinder - Words to Pi Value Worksheet

| Math worksheet on 'Surface Area - Cylinder - Words to Pi Value (Level 1)'. Part of a broader unit on 'Geometry - Volume and Surface Area of Complex 3D Shapes - Advanced' Learn online: app.mobius.academy/math/units/geometry_complex_3d_shapes_advanced/ |
1
| What is the surface area of this shape? |
| A Cylinder with radius 2 and height 5 |
a

b

2
| What is the surface area of this shape? |
| A Cylinder with radius 4 and height 2 |
a

b

3
| What is the surface area of this shape? |
| A Cylinder with radius 3 and height 5 |
a
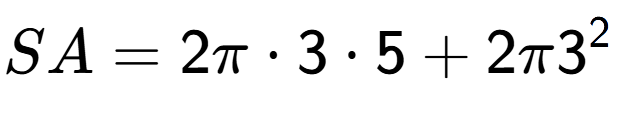
b
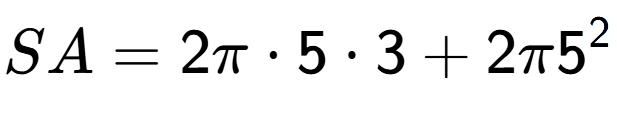
4
| What is the surface area of this shape? |
| A Cylinder with radius 2 and height 4 |
a

b

5
| What is the surface area of this shape? |
| A Cylinder with radius 5 and height 4 |
a
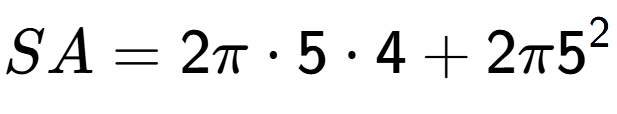
b
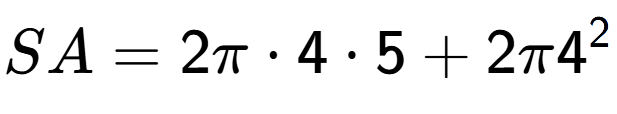
6
| What is the surface area of this shape? |
| A Cylinder with radius 4 and height 5 |
a

b

7
| What is the surface area of this shape? |
| A Cylinder with radius 3 and height 2 |
a
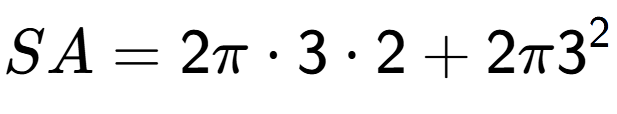
b