This topic revolves around calculating the volume of cones, applying the formula \( V = \frac{1}{3} \pi r^2 h \), where \( V \) is the volume, \( r \) is the radius, and \( h \) is the height. Various problems provide specific dimensions of cones and require the learner to compute their volumes using values of \(\pi\). Also included are multiple-choice answers to confirm understanding, highlighting typical computational errors or misconceptions by offering incorrect alternatives. This practice is part of an advanced study unit focused on the volume and surface area of complex three-dimensional shapes.
Work on practice problems directly here, or download the printable pdf worksheet to practice offline.
moreVolume - Cone - Words to Pi Value Worksheet

| Math worksheet on 'Volume - Cone - Words to Pi Value (Level 1)'. Part of a broader unit on 'Geometry - Volume and Surface Area of Complex 3D Shapes - Advanced' Learn online: app.mobius.academy/math/units/geometry_complex_3d_shapes_advanced/ |
1
| What is the volume of this shape? |
| A Cone with radius 3 and a height of 5 |
a
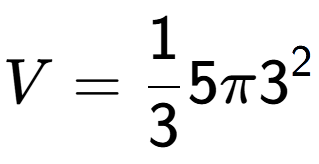
b
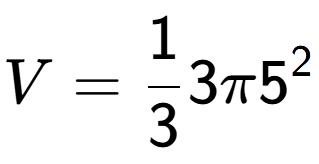
2
| What is the volume of this shape? |
| A Cone with radius 5 and a height of 3 |
a

b

3
| What is the volume of this shape? |
| A Cone with radius 4 and a height of 5 |
a
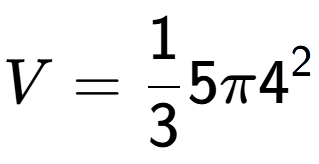
b
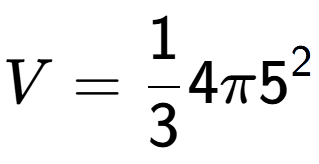
4
| What is the volume of this shape? |
| A Cone with radius 4 and a height of 3 |
a
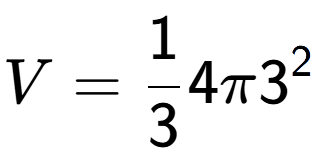
b
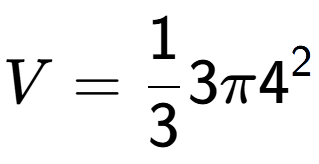
5
| What is the volume of this shape? |
| A Cone with radius 2 and a height of 4 |
a
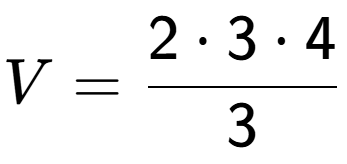
b
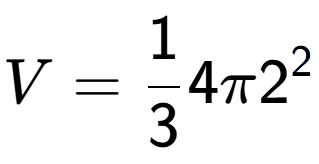
6
| What is the volume of this shape? |
| A Cone with radius 5 and a height of 4 |
a

b

7
| What is the volume of this shape? |
| A Cone with radius 2 and a height of 3 |
a

b
